Modeling of Type 3 Wind Turbine Generators

Author: National Renewable Energy Laboratory^[1]

To model a wider variety of faults (such as faults internal to the wind power plant) and wind power plant and turbine protection, a detailed representation of a DFIG turbine, with electrical machine and power electronics explicitly modeled, is necessary, especially to demonstrate the DC bus dynamics and protection of power semiconductor devices which may require the use of a “crow-bar” to limit the DC bus currents during a fault. The model described here is an evolution of the fixed-speed (Type 1) and variable-slip (Type 2) models. It incorporates many of the same subsystems as those models, while power electronic converters for decoupled real and reactive power control and maximizing of extraction of power from the wind.
The complete model has been implemented in PSCAD/EMTDC for the purposes of this article. However, the model is straightforward to implement using other popular simulation packages such as MATLAB/Simulink. The model is based on parameters from a GE 1.5-MW turbine.

Model Development

Turbine Properties
Turbine make	GE 1.5MW
Regulation method	Pitch control (disabled)
Rotor diameter	70.5 m
Hub height	65 m
Number of blades	3
Cut-in wind speed	4 m/s
Cut-out wind speed	20 m/s
Rated wind speed	12 m/s (13 m/s used)
Rotor speed	11/22 rpm

Wind turbines are complex electromechanical devices and incorporate a large number of controls. In order to tackle complexity, wind turbines can be thought of as a collection of subsystems which can be modeled individually. The individual subsystem models can then be assembled into a complete wind turbine model. From a modeling standpoint, a full converter permanent magnet alternator (PMA) wind turbine consists of the following mechanical and electrical subsystems:

• Aerodynamic model for rotor;
• Mechanical two-mass model for drivetrain;
• Reference power calculation block;
• Pitch controller;
• Induction generator model;
• Rotor-side converter;
• Grid-side inverter;
• Unit transformer and grid representation.

The interaction between each of the components listed above determines the wind turbine model’s steady-state and dynamic response. Modeling of the aerodynamics and mechanical drive-train is based on the differential and algebraic equations that describe their operation. Reference power is currently calculated based on wind speed, though in the future it will be calculated based on rotor speed. The pitch controller currently utilizes both power and rotor speed inputs, though it too will be modified in the future to only use rotor speed as input. The induction generator model (available in PSCAD/EMTDC) has been modified to serve the purposes of this model. The machine-side converter and grid-side inverter are modeled explicitly using diode and IGBT models supplied in PSCAD/EMTDC. Details for each of the subsystems are presented in the following subsections.

Aerodynamic Block

The aerodynamic block consists of three subsystems: tip-speed ratio calculation, rotor power coefficient (C_P) calculation, and aerodynamic torque calculation. Wind speed and pitch angle are user-defined inputs. Since the model is intended to study the dynamic response of wind turbines to grid events, the assumption is usually made that the wind speed stays constant during the grid event. However, this model allows the wind speed input signal to be set to any value at the start of the simulation run-time and also to be modified during the run. It is also possible to use a time-series of actual wind speed data.

Tip-Speed Ratio Calculations

The tip-speed ratio or TSR, denoted by λ, is the ratio of the blade-tip linear speed to the wind speed^[2]. The TSR determines the fraction of available power extracted from the wind by the wind turbine rotor. The TSR can be calculated as follows

\(\lambda=\frac{\omega_{rotor} · R_{rotor}}{V_{wind}}\)

where,
ω_rotor = rotor angular speed [rad/s]
R_rotor = rotor radius [m]
V_wind = wind speed [m/s]

Rotor Power Coefficient (C_p) Calculation

The TSR, together with the user-defined blade pitch angle β, are used to calculate the rotor power coefficient, denoted by C_P. The rotor power coefficient is a measure of the rotor efficiency and is defined as

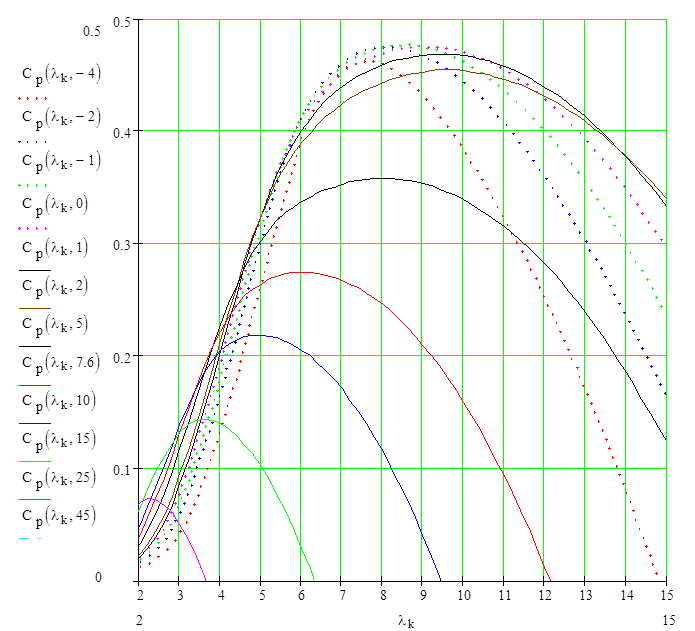
\(\mathrm{C}_P=\frac{Extracted\ Power}{Power\ in\ Wind}=\frac{P_{rotor}}{P_{wind}}\)

There is a constant value of λ which, if maintained for all wind speeds, will result in an optimal C_P curve and optimal power extraction from the wind. Variable-speed wind turbines are equipped with a pitch-change mechanism to adjust the blade pitch angle and obtain a better power coefficient profile. In the model, a set of generic C_P curves are used to calculate the value of C_P^[3].

Aerodynamic Torque Calculation

The kinetic energy E (in J) of an air mass m (in kg) moving at a speed V_wind (in m/s) is given by^[2]

\(E=\frac{1}{2}mV_{wind}^2\)

If the air density is ρ (kg/m³), mass flow through an area A is given by

\(\dot{m}=ρAV_{wind}\)

Thus, an equation for the power (in W) through a cross-sectional area A normal to the wind is

\(P_{wind}=\frac{1}{2}ρAV_{wind}^3\)

In the case of a wind turbine, area A is the area swept by the rotor blades. Only a part of this power may be captured due to the non-ideal nature of the rotor, hence the need for the coefficient C_P.

\(P_{rotor}=\frac{1}{2}ρ\cdot\mathrm{C}_p\cdotπ\cdot\mathrm{R}_{rotor}^2\cdot\mathrm{V}_{wind}^3\)

The aerodynamic torque developed (in Nm) can then be calculated

\(\Gamma_{rotor}=\frac{P_{rotor}}{ω_{rotor}}=\frac{\frac{1}{2}\cdotρ\cdot\mathrm{C}_p\cdotπ\cdot\mathrm{R}_{rotor}^2\cdot\mathrm{V}_{wind}^3}{ω_{rotor}}\)

Mechanical Drive-Train

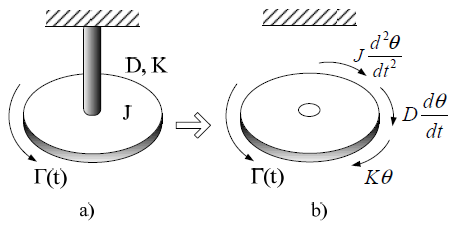
The mechanical block consists of the rotor shaft, generator shaft, and a gearbox. The shafts and the gearbox are modeled using a two-mass inertia representation. For a rotational system^[4], consisting of a disk with a moment of inertia J mounted on a shaft fixed at one end, let us assume that the viscous friction coefficient (damping) is D and that the shaft torsional spring constant (stiffness) is K. The torque acting on the disk can be calculated from the free-body diagram of the disk, as follows

\(\Gamma(t)=J\frac{d^2\theta(t)}{dt^2}+D\frac{d\theta(t)}{dt}+K\theta(t)\)

A more complex rotational system consists of two such systems. The two systems are coupled through a gear train, and Γ is the external torque applied to the disk of System 1. Γ₁, Γ₂ are transmitted torques. N₁, N₂ are the numbers of teeth of Gear 1 and Gear 2. J₁, J₂, D₁, D₂, K₁, K₂ are the moments of inertia, damping, and stiffness of System 1 and System 2, respectively. The system is still time-dependent, but the notation t is dropped for the sake of clarity.

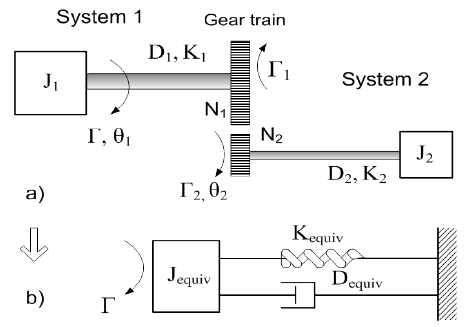
The torque equation at J₁ can then be calculated as

\(\Gamma_1=J_1\frac{d^2\theta_1}{dt^2}+D_1\frac{d\theta_1}{dt}+K_1\theta_1\)

The torque equation at J₂ can then be calculated as

\(\Gamma_2=J_2\frac{d^2\theta_2}{dt^2}+D_2\frac{d\theta_2}{dt}+K_2\theta_2\)

Since Γ₁ = (N1/N2)Γ₂ and Θ₂ = (N1/N2)Θ₁, the quantities on Gear 2 side can be referred to the Gear 1 side^[4].

\(\Gamma_1=\left (\frac{N_1}{N_2} \right)\left (J_2\frac{d^2\theta_2}{dt^2}+D_2\frac{d\theta_2}{dt}+K_2\theta_2 \right)\) \(\Gamma_1=\left (\frac{N_1}{N_2} \right)\left [J_2\left (\frac{N_1}{N_2} \right)\frac{d^2\theta_1}{dt^2}+D_2\left (\frac{N_1}{N_2} \right)\frac{d\theta_1}{dt}+K_2\left (\frac{N_1}{N_2} \right)\theta_1 \right]\) \(\Gamma_1=J_{refl}\frac{d^2\theta_1}{dt^2}+D_{refl}\frac{d\theta_1}{dt}+K_{refl}\theta_1\)

where J_refl, D_refl, and K_refl are the quantities reflected on the Gear 1 side. Substituting the above equations and rearranging them, we obtain the equation for the applied torque. The gear train is eliminated in the equivalent system.

\(\Gamma=J_{equiv}\frac{d^2\theta_1}{dt^2}+D_{equiv}\frac{d\theta_1}{dt}+K_{equiv}\theta_1\)

where,

\(J_{equiv}=J_1+J_2\left (\frac{N_1}{N_2} \right)^2=J_1+J_{refl}\) \(D_{equiv}=D_1+D_2\left (\frac{N_1}{N_2} \right)^2=D_1+D_{refl}\) \(K_{equiv}=K_1+K_2\left (\frac{N_1}{N_2} \right)^2=K_1+K_{refl}\)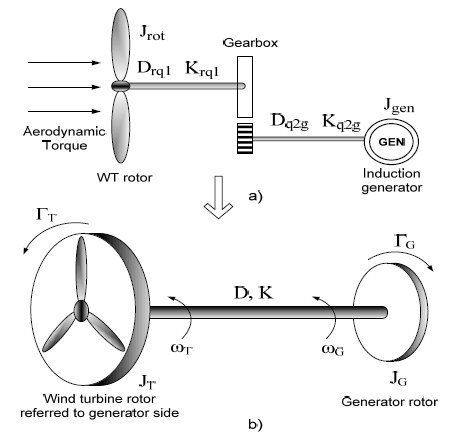

The wind turbine drive-train can therefore be modeled as a two-mass system coupled through a gear train. The quantities on the wind turbine rotor side of the gearbox can be reflected to the generator side. This eliminates the gear ratio and results in a two-mass representation of the wind turbine. Neglecting the effects of the gearbox moment of inertia, damping, and stiffness is justifiable since the moment of inertia of the wind turbine rotor is comparatively very high.
Torque equations representing the mechanical behavior of the wind turbine are derived, based on the two-mass model. The aerodynamic torque from the wind turbine rotor and the electromechanical torque from the direct-connect induction generator act in opposition to each other. Torque equations with all quantities referred to the generator side are

\(J_T\ddot {\theta_T}+D(ω_T-ω_G)+K(\theta_T-\theta_G)=\Gamma_T\) \(J_G\ddot {\theta_G}+D(ω_G-ω_T)+K(\theta_G-\theta_T)=-\Gamma_G\)

where,
J_T, J_G = moments of inertia of the wind turbine rotor and the generator [kgmm]
Γ_T, Γ_G = wind turbine aerodynamic and generator electromagnetic torque [Nm]
ω_T, ω_G = wind turbine rotor and the generator speed [rad/s]
Θ_T, Θ_G = angular position of the rotor and the generator [rad]
D, K = equivalent damping and stiffness [Nms/rad], [Nm/rad]
Speeds and torques of the turbine rotor and the generator can be determined for each simulation time step by solving the above equations using a state-space approach. The state-space equations are

\(\frac{d}{dt}(\theta_G-\theta_T)=(ω_T-ω_G)\) \(\dot {\omega_T}=\left (\frac{1}{J_T} \right)\left [\Gamma_T-D(\omega_T-\omega_G)-K(\theta_T-\theta_G) \right]\) \(\dot {\omega_G}=\left (\frac{1}{J_G} \right)\left [D(\omega_T-\omega_G)+K(\theta_T-\theta_G)-\Gamma_G \right]\)

Reference power calculation

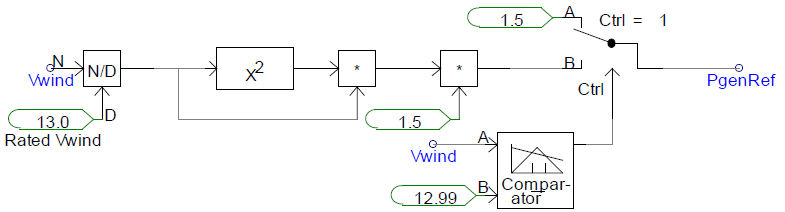
The reference power calculation is based on user-defined wind speed. Wind speed is per unitized based on rated wind speed, cubed and multiplied by rated power (1.5 MW) to get output power. If user-defined wind speed exceeds rated wind speed (13 m/s), output power is fixed to 1.5 MW.

Pitch control block

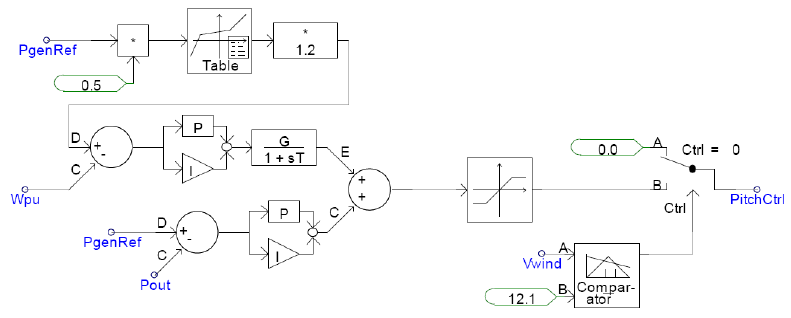
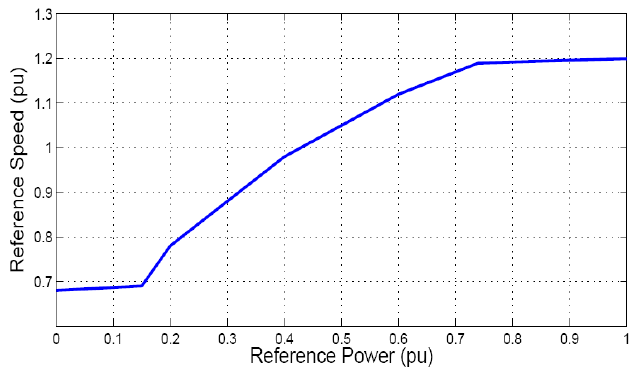
The pitch control block changes blade pitch angle at higher than rated wind speeds to spill excess power. Thus, power output is maintained at rated value even though wind speed exceeds rated wind speed. In this particular implementation, reference power is per unitized and converted to reference speed based on a look-up table. A multiplier after the look-up table is included to maintain stability. The reference speed and actual speed are compared and error drives upper PI controller. Reference power and actual power are also compared and error drives the lower PI controller. PI controller outputs are summed and hard-limited to generate the pitch angle signal. The pitch angle signal is active only when wind speed is close to rated, and otherwise is fixed at zero.

Induction Generator

DFIG wind turbines employ wound-rotor induction machines, for which models are readily available in most power system modeling software. The platform of choice to implement the model was PSCAD/EMTDC, and the in-built wound-rotor induction machine model was used. Alternatively, if the modeling platform does not offer a built-in model, users may develop third or fifth-order algebraic models for induction machines based on the literature available^[5].

Induction generator ratings
Rated MVA	1.5 MVA
Rated Voltage	0.575 kV line-to-line
Number of poles	6
Rated frequency	60 Hz
Stator/rotor turns ratio	0.379
Induction generator parameters
Stator winding resistance	0.0071 pu
Wound rotor resistance (int)	0.005 pu
Stator leakage inductance	0.1714 pu
Squirrel-cage inductance	0.1563 pu
Magnetizing inductance	2.9 pu
Angular moment of inertia	0.5 s

Rotor and Grid Side Converter Control for DFIG

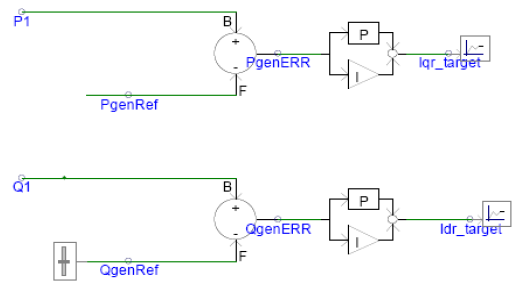
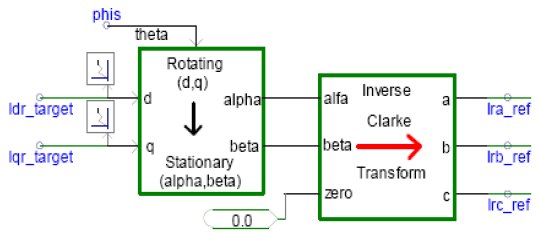
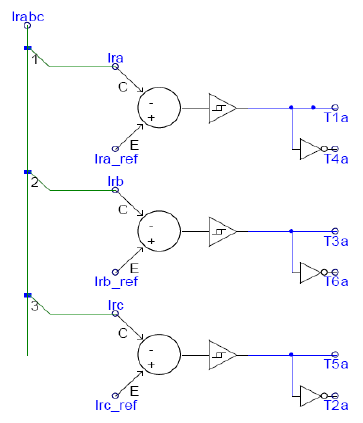
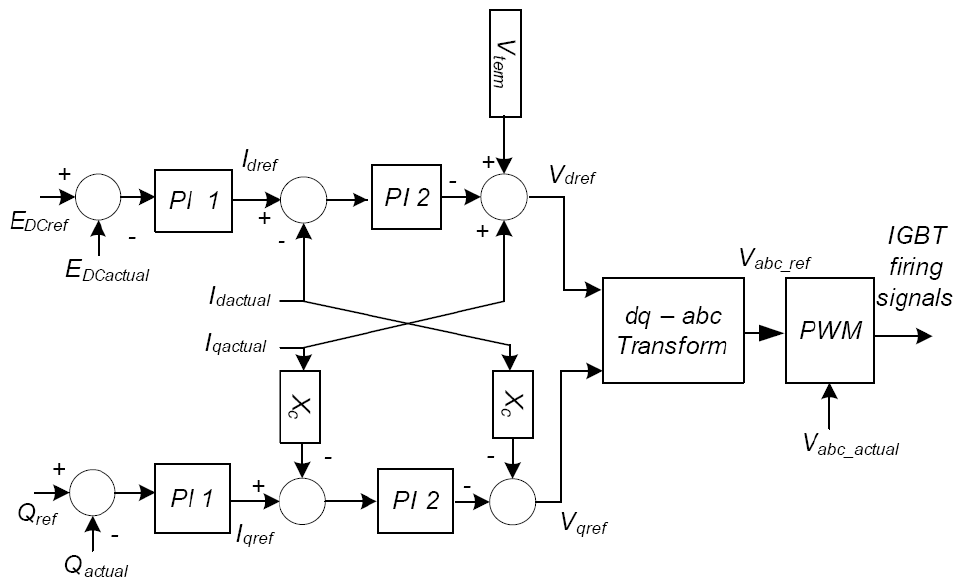
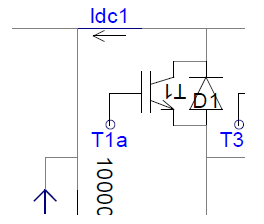
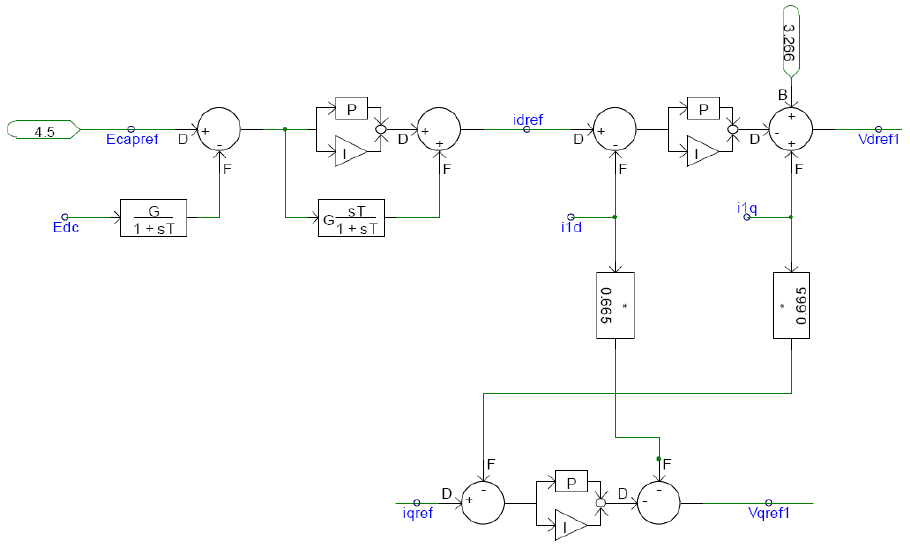
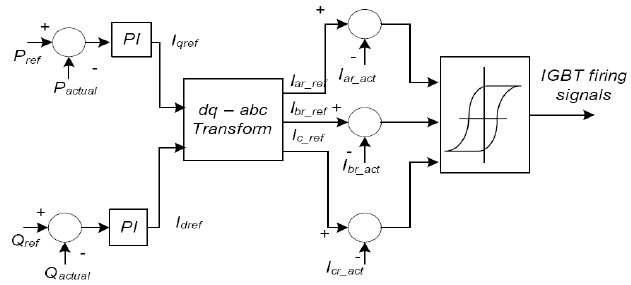
The rotor-side converter of the DFIG is connected to the grid-side converter through a DC link capacitor. Assuming that the grid-side converter maintains a constant DC-link voltage, the role of the rotor side converter is to inject rotor frequency (variable) currents into the rotor circuit in such a manner as to achieve decoupled active and reactive power control. Since the converter operates in a stator-flux qd0-reference frame, the rotor current is decomposed into an active power (q-axis) and a reactive power (d-axis) component. With change in wind speed, slip changes and thus the frequency of rotor currents^[5][6]. Actual active power (P_gen) is compared with the set point value (P_genref) which is determined by the wind speed. A PI controller is used to generate the required value of q-axis rotor current I_qr. Similarly, for reactive power, a PI controller is used to generate the required d-axis rotor current I_dr^[7]. The proportional gain (Kp) and integral gain (Ki) constants for the PI controller are determined using the Ziegler-Nichols method^[8]. These values of I_qr and I_dr are transformed back into the abc frame to obtain the required value of rotor currents. Hysteresis controller used to generate the switching sequence for the IGBT switches in the rotor-side converter. Required rotor currents obtained in abc frame are thus generated by using hysteresis control.
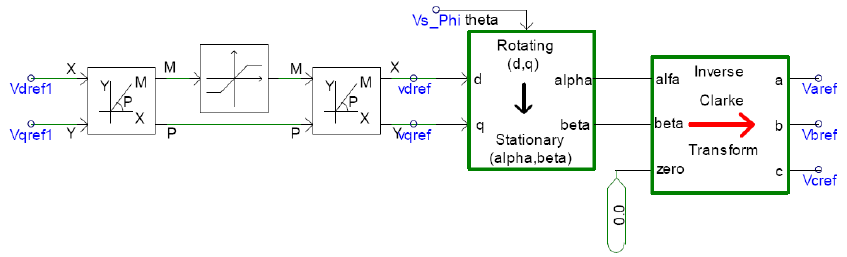
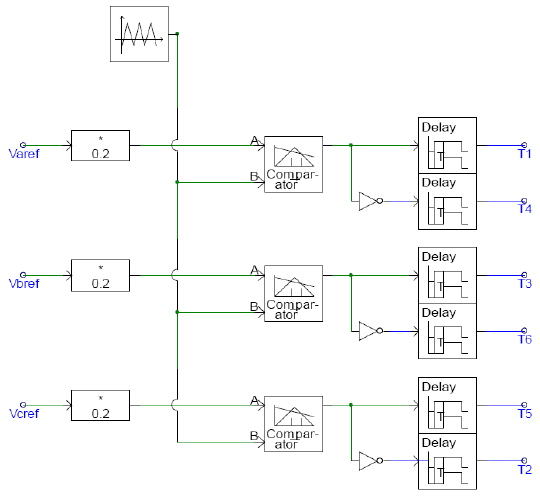
The grid side converter is responsible for balancing power injected into the DC link capacitor versus active power exchanged with the grid^[5][6]. The converter at the grid side is controlled in a manner so as to achieve constant link voltage across the DC link capacitor. A relation between the DC link voltage and the qd0−axis stator currents and stator voltages is used to model the control and firing circuit for the grid-side converter. Field-oriented control, using Clarke and Park transforms, is used to obtain the actual qd0−axis stator currents and stator voltages. The desired qd0 voltages to keep the DC link voltage constant, are obtained by comparing the actual value of the DC link voltage. PI controller is used to obtain the desired values of the stator voltages in qd0 frame. The proportional gain (Kp) and integral gain (Ki) constants for the PI controller were determined using the Ziegler-Nichols method. These desired qd0 voltages are then transformed to abc frame by applying the inverse Park-Clarke transforms to fire the IGBTs.

Crowbar Protection for Rotor Circuit

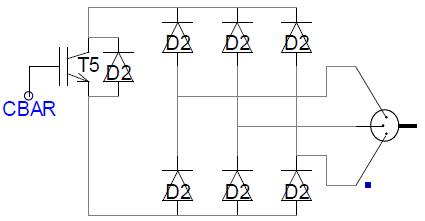
This model includes a “crowbar” circuit^[9] that shorts the rotor windings of the induction generator in the event of detection of high currents in the rotor circuit. This protects the rotor-side converter from over-currents. Signal CBAR goes high if over-current is detected (in our case, if rotor currents exceed 4 pu) and triggers the crowbar circuit.

Unit Transformer and Grid Representation

The unit transformer and grid are both modeled using in-built blocks supplied by PSCAD/EMTDC. The unit transformer is a wye-delta 2-MVA transformer with a primary voltage of 34.5 kV and a secondary voltage of 0.6 kV, and a per unit leakage reactance of 0.1 p.u. During the development and testing phase, the grid is represented by a 34.5-kV voltage source.

Complete Model Implemented in PSCAD/EMTDC

 

 

Model Testing

The model testing phase is essential to evaluate the capabilities of the model. The model testing phase has three main objectives:

• To verify that desired wind turbine power curve is achieved;
• To demonstrate independent real and reactive power control;
• To demonstrate pitch controller action.

If the model is able to meet these objectives, we can use it with confidence as a platform for modeling more advanced controls, such as providing inertia and frequency response.

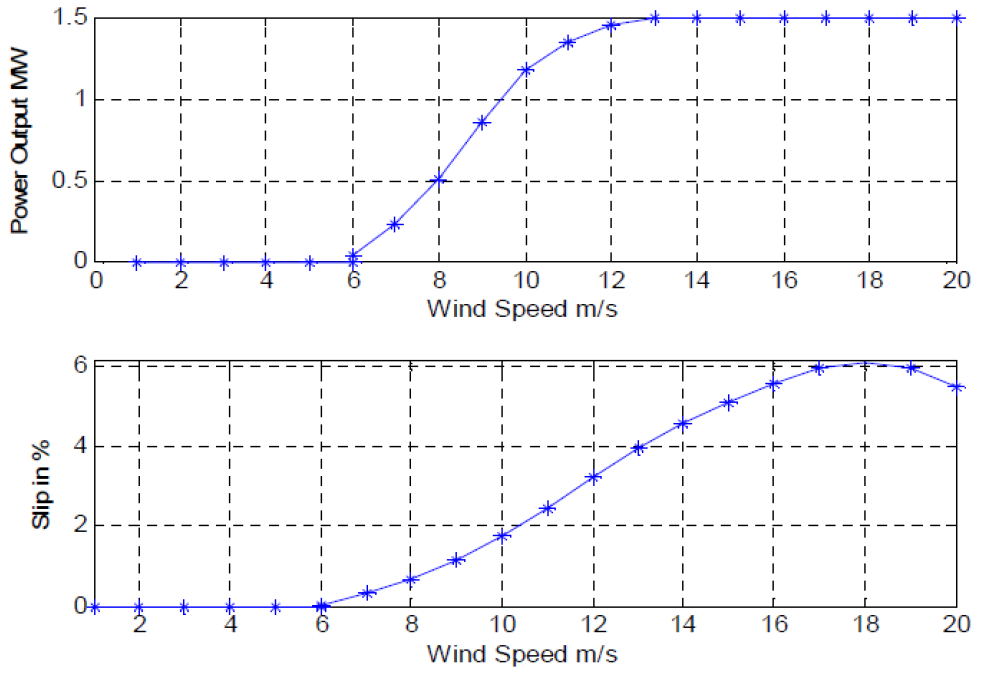
Power Curve

The desired power curve is a cubic function of per unit wind speed (up to rated wind speed). Rated power is achieved at rated wind speed. Beyond rated wind speed, the desired power is flat at rated power. Thus, the curve has a sharp edge at rated wind speed. The power output tracks the desired curve closely. The plot is obtained from a PSCAD/EMTDC simulation multi-run to ensure that the power output measured for each wind speed is the steady-state value. Thus, we can claim that that the first objective, that of achieving the desired power curve, is met.

 

Data for power curve and slip Vwind (m/s) Pout (MW) Slip (%) 6 0.035 -0.01 7 0.233 -0.32 8 0.501 -0.68 9 0.850 -1.16 10 1.181 -1.76 11 1.344 -2.44 12 1.451 -3.23 13 1.5 -3.96 14 1.5 -4.55 15 1.5 -5.08 16 1.5 -5.56 17 1.5 -5.95 18 1.5 -6.10 19 1.5 -5.97 20 1.5 -5.48

 

Independent Real and Reactive Power Control

To test if independent real and reactive power control has been achieved, four tests were carried out: real power drop, reactive power drop, real power rise, and reactive power rise. Each of these is modeled as a step change, i.e., at a particular instant, the simulation was paused and a step change was made to either the wind speed or reactive power demand. In the first test, a real power drop was simulated. The wind speed was changed from 14 m/s to 8 m/s at t=13s. The reactive power demand was set at 0.4 MVAR. The real power output drops and settles to the new value. Reactive power drops initially but recovers to the original value. In the second test, a reactive power drop was simulated. The wind speed remains at 14 m/s throughout the run, but reactive power demand was changed from 0.4 MVAR to 0.0 MVAR at t=17s. The reactive power dropped, as expected. The real power output shows a slight perturbation but recovers to the original value. In the third test, a real power rise was simulated. The wind speed was changed from 8 m/s to 14 m/s at t=14s. The reactive power demand was set at 0.5 MVAR. The real power output rises and settles to the new value. Reactive power rises initially but recovers to the original value. In the fourth test, a reactive power rise was simulated. The wind speed remains at 13 m/s throughout the run, but reactive power demand was changed from 0.0 MVAR to 0.4 MVAR at t=11s. The reactive power rose, as expected. The real power output once again shows a slight perturbation but recovers to the original value.

 

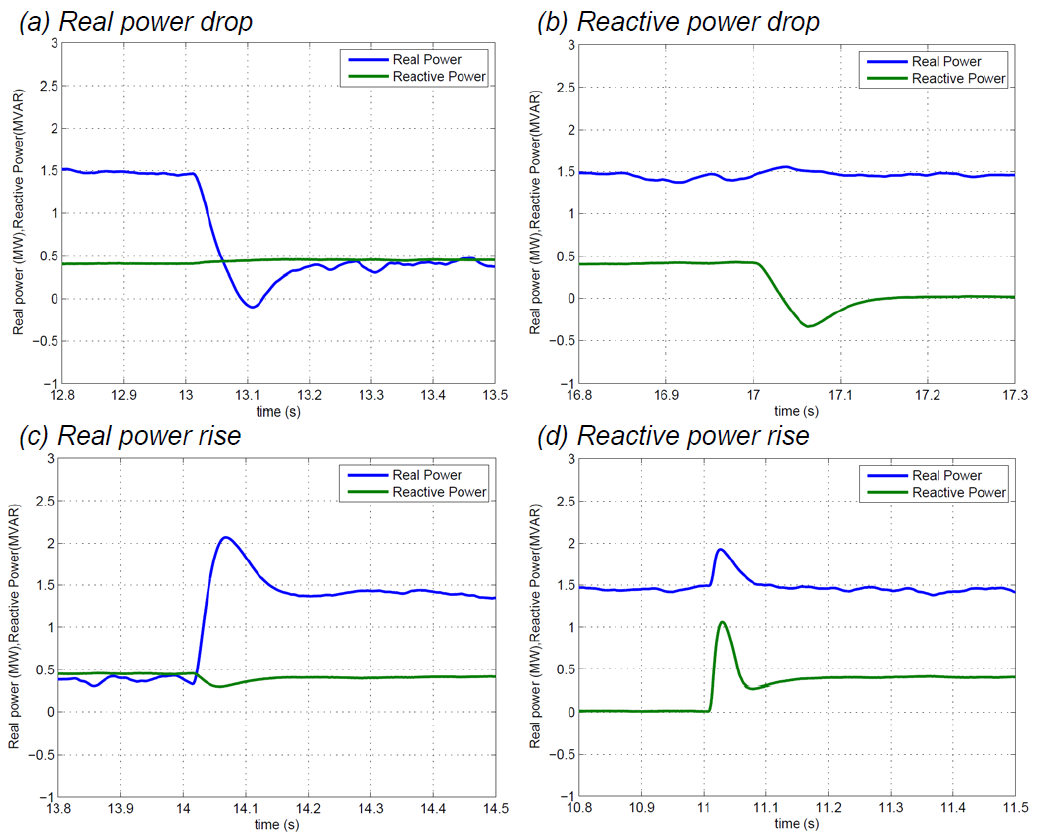Consider the real power drop. In this case, when wind speed drops suddenly, the pitch controller is de-activated, and the pitch angle moves quickly to zero. This is likely the cause for the overshoot observed in the power waveform. Within the wind turbine control system, the change in wind speed changes the P_genref value. At this instant, the error between P_genref and the actual power output becomes large, driving a change (reduction) in the value of q-axis current Iq. The d-axis current does not change since the reactive power set-point is not changed. This change in Iq leads to a corresponding change in the three-phase currents, leading to the desired change in the real power output. The reason the reactive power output briefly jumps is likely that the decoupling technique is intended to work in steady-state rather than in the transient domain, and a surge in real power causes a rapid change in the flux linkages within the machine, which affect the reactive power. However, the reactive power controller detects this condition and corrects it. The results conclusively show that a change in either real power or reactive power demand does not affect the other quantity except momentarily. Based on the results of the testing, we can claim that the objective of independent real and reactive power control has been achieved.

Pitch Control

A test was devised to evaluate pitch controller action. The wind speed changed from 11 m/s to 15 m/s at t=25s. The pitch angle was initially at 0 degrees (i.e., the pitch controller was inactive). From the obtained results, it can be seen that the pitch controller becomes active when wind speed change occurs. This occurs due to new wind speed (15 m/s) being higher than rated. Eventually, the pitch angle settles close to -8 degrees, effectively spilling some excess power. The test shows that the pitch controller does indeed work in a stable fashion.

 

 

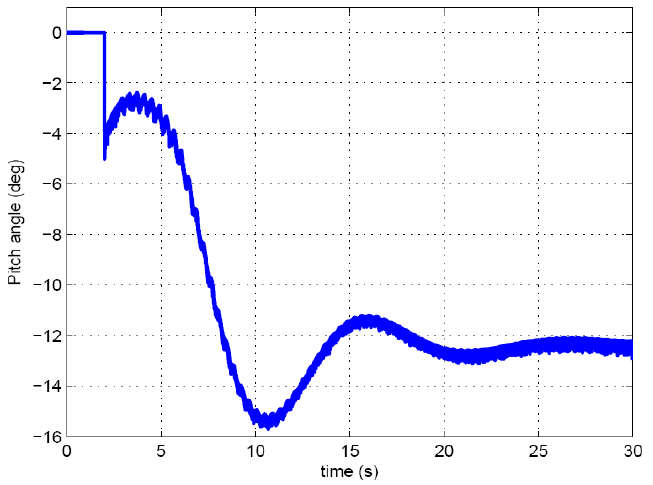Dynamic Response

To demonstrate the model’s ability to reproduce wind turbine dynamics, a test was created. The wind turbine was operated with a constant wind speed (13 m/s). This wind speed was chosen to be the rated value. A voltage sag on the grid was simulated, and the real and reactive power response of the wind turbine was observed. Note that this is not an implementation of low-voltage ride through (LVRT) but rather a test of dynamic response. The grid voltage drops gradually in this case from 1 p.u. to 0.8 p.u. at t=25s, and the sag persists for 18 cycles (0.3 seconds). A “V-shaped” sag is observed. The intent of the test is to show that the model does indeed respond to events occurring in the dynamic timescale and that the response of the machine to this event is realistic. Obtained results show that the model does indeed respond to the grid event as expected.

 

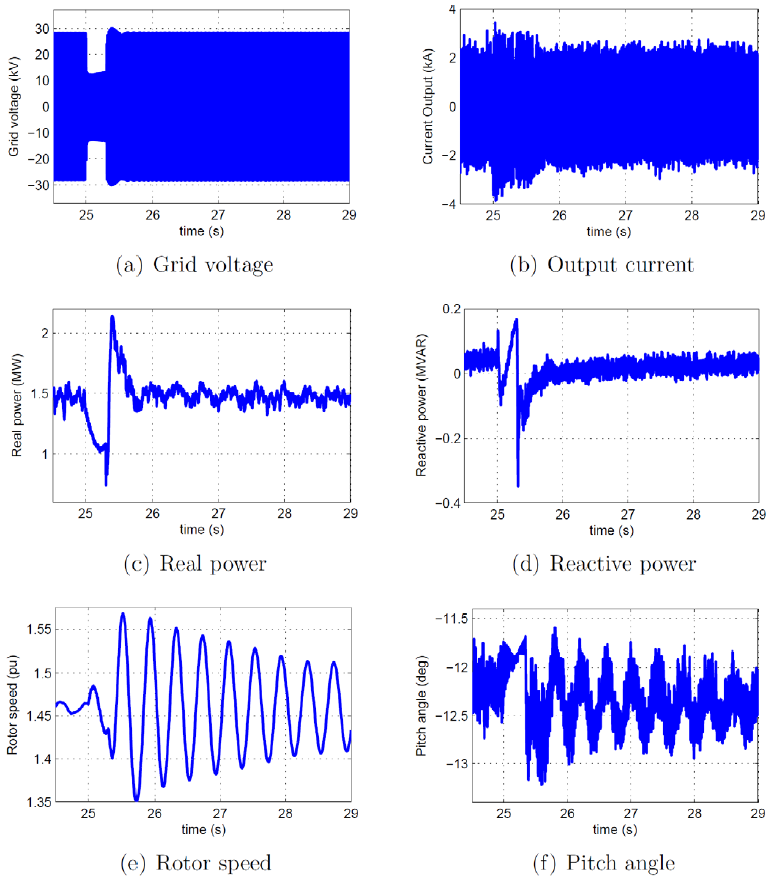Real and reactive power show a sharp drop when the event starts. The converter then increases the current demand from the generator, which reflects as a jump in power. The pitch controller too seeks to maintain real power output at 1.5 MW. A considerable excursion occurs in the rotor speed, but it is eventually damped out. Based on these results, we can say that the model is behaving as expected, and realistic explanations for the response can be offered.

References